文章内容在此处输出。小学数学的数方格启蒙
小学时,数学课通常从数方格入手。老师会在黑板上展示一张大纸,上面密密麻麻都是小方格。他会向学生解释,每个小方格的边长都是1厘米,这些小方格拼在一起就构成了1平方厘米的面积。刚开始学习多边形面积时,就是通过数这些小方格来完成的。孩子们通过这种方法,慢慢了解并掌握了复杂世界的规律,学会了算术和对称等基本概念,从而开启了他们的数学学习之路。
数方格看似简单,却是小学生学习数学的起点。在这个过程中,孩子们慢慢学会用数学的眼光去分析和理解图形与数字间的联系。这为他们日后更深入的数学学习打下了基础,对他们形成基本的数学思维和技能有着极大的帮助。
线段精确长度的困境
绘图时,我们可能会遇到一些难题。比如,用直尺画线段,常常难以精确量取其长度。这个问题虽然看似简单,实则对“数值与图形相匹配”的传统认识提出了挑战。
现在这或许不算什么严重问题,但在过去,它却引发了巨大的认知难题。眼前虽然看到了线段,却无法确切了解其具体数值,这让很多人感到困惑,对数学的准确性产生了怀疑。
无理数√2 的诞生
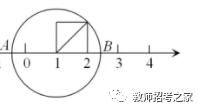
古希腊两千多年前,毕达哥拉斯定理刚被提出,其学派里有个叫希帕索斯的成员就有了惊人发现。他研究边长为1的正方形对角线长度时,发现了无理数√2。这个发现直接影响了毕达哥拉斯学派对数学的看法。
该学派坚信,无论数量多少,只要有足够的精确度,都能用有理数来描述。但√2的出现,却打破了这一信念。√2无法用有理数精确表示,这使得毕达哥拉斯学派的理论根基受到严重打击,他们的数学信念就像一座即将倒塌的高楼。
第一次数学危机
希帕索斯发现了根号二这个无理数,这一发现引发了数学史上所谓的“第一次危机”。当时,人们普遍认为所有数字都能用有理数来表示。在古希腊,几乎所有人都这么认为。即便在测量技术高度发达的今天,仍有很多人坚持这种看法。
一些对毕达哥拉斯学说狂热追随者,对新颖理论难以接受,竟然将希帕索斯装进麻袋,扔进了鱼群。尽管如此,问题依旧没有得到解决。这次事件让人们意识到数学并非完美,同时也激发了数学家们去寻找新的数学理论。
圆的精确数值难题
即便时至今日,数学领域仍面临诸多难题。尝试将圆形物体切开并拉成直线,即便是最尖端的测量设备,也难以精确测量其长度。面对这些资料,我们仿佛遭遇了挑战,心头不禁感到困惑。
数学家们对此问题长期感到迷茫。但到了19世纪,德国的康托尔提出了关于超穷数的理论。这一理论使人们对无穷大的认识有了全新的突破。依据此理论,无理数在数轴上的分布比有理数更为密集。在数轴上随机选取一点,几乎很难遇到有理数。
自然数奇偶数量之惑
小学生都能理解的一个疑问是:在自然数里,奇数和偶数哪个数量更占优势?有人认为自然数的总和就是奇数与偶数相加的结果,似乎它们数量相当。但实际上,这里涉及到了相当复杂的数学集合理论。
这个问题看似简单,实则深藏着集合之间比较的复杂性。很多人都知道答案可能不简单,但对它的深层意义还是感到迷茫。关于这个问题的讨论一直持续不断,那么,你的看法是什么?欢迎在评论区分享你的观点,同时请不要忘记点赞和转发这篇文章!